Four fours
Another old puzzle that I saw somewhere recently is the four fours problem. The task is to find mathematical expressions using only four fours which result in all numbers between 0 and 100. The beginning of the list looks something like this:

The basic operations are $ + - \times{} \; / $, decimal dot ($.4 , 4.4$), recurring decimal ($ .\overline{4} = .444444… = \frac{4}{9} $), square root, exponentiation and factorial. But with these operations, one reaches pretty quickly the first number which is not reachable. Therefore, the operations are extended to less common things like n-th root, gamma function, percent function and bitwise operations like and, or, xor and shift.
Logarithms are not in the list of a good reason. With this formula
every number can be reached just by adding the right amount of roots.
In this paper, David Wheeler explains the rules and lists the solutions he found for numbers below 40’000.
I found it interesting enough to play with this puzzle during a weekend. The basic algorithm to find the solutions is pretty simple and explained on the wikipedia page.
I implemented a version in Kotlin the new JVM language by Jetbrains, the creators of IntelliJ IDEA. Not surprisingly, the IDE support is very good and the language is relatively simple yet modern. Given some experience in Java, one can get productive without any big introduction.
The first version was quickly done and worked ok. But soon enough, the devil came out of the details and gave me some tricky issues to solve.
A typical critical point in such applications is to keep the search space as small as possible to avoid a combinatorial explosion.
The concrete problem here is that unary operands (roots or factorials etc.) can be applied infinitely many times to every term in an expression. Factorials, exponentials and others produce bigger numbers than their inputs, so these functions are only applied to small enough terms.
But the root function creates smaller values and therefore, no limit can be set on the input. As a solution, I use rational numbers and only apply roots to numbers if the result is still rational. Second, I set an arbitrary limit on the number of consecutive applications of a function, expressions like $ \sqrt{\sqrt{\sqrt{4^2}^2}^2} $ are not expanded further after a given amount of steps.
Another problem are silent integer overflows of the JVM. This creates subtle bugs without any error message. Since 1.8, JDK provides methods like multiplyExact which seams a perfect fit. But it throws an exception in case of an overflow. This is terrible for the performance. So I copied the code and changed it to return null in case of an overflow.
The clean, nice code from the beginning was vanishing behind workarounds and null checks. But life is not Disney land.
With a running program I could make some experiments. It found different and more solutions than David Wheeler. It found solutions for all numbers below 40’000 except for 395 numbers, starting with 9’707, 11’307, 12’107, 17’123, 17’531, 17’623, …
Then I tried to find solutions not for fours but for the other digits.
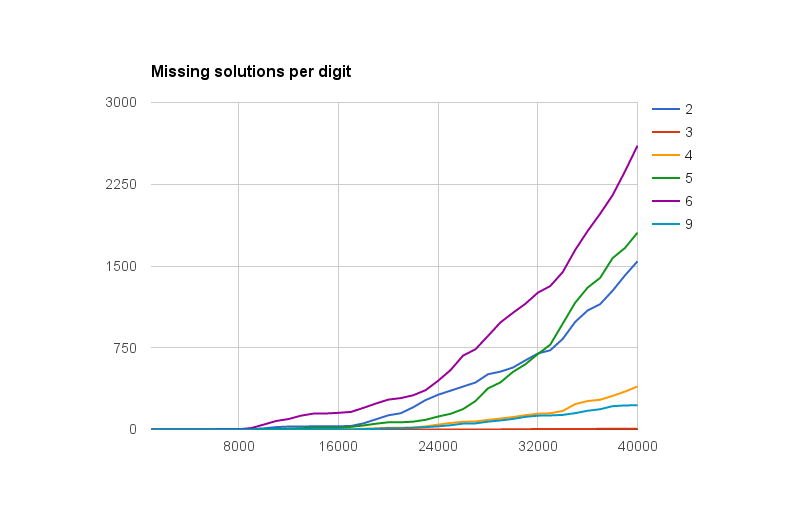
It turns out that fours are only the third best take. Four threes can build almost every number below 40’000. Just six are missing: 25’163, 29’543, 29’557, 31’307, 34’763, 36’683. Also four nines can build more numbers than fours. The digits 1, 7 and 8 behave much worse with an amount of missing numbers between 10’000 and 33’000.
The full data (although not nicely formatted) is available here: ones - twos - threes - fours -
fives - sixes - sevens - eigths - nines -
Interestingly, 40’000 can be built out of every digit, most with pretty simple formulas:
It was another mathemagical weekend.